Exam #2 Solutions
1. One example would be the unit interval T = (0, 1) which is bounded and
open, and the sequence (xn) = (1/n)
which has no subsequence converging to a limit in T (since the sequence
converges to
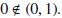
2. The union of two closed sets is closed. If p is a limit point of one of
the two sets, it is still a limit point of
their union (every neighborhood of p will contain points other than p from the
one set and thus from the union).
Therefore the union will always be perfect.
3. Assume without loss of generality that x < y. Since the rational numbers
are dense in the real numbers, there is
a rational number q such that x < q < y. Let A be the irrational numbers less
than q and B the irrational numbers
greater than q.
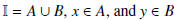by the way we defined A and B.
A and B are disjoint.
The limit points of A are (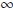
,
q] and the limit points of B are [q,
).
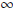A contains no limit points of B and vice
versa.
A and B are separated.
4. Each set Xn = (−n, n) is bounded but the union for all n ∈ N is R, which is unbounded
5. An interval is a nonempty set I such that if x < y are both in I and x < z
< y then z ∈ I. Since 0 and 1 are in the
Cantor set but 1/2 is not, the Cantor set is not an interval.
6. A point is a limit point of a set if we can construct a sequence of points
in the set not equal to the limit point that
converge to it.
For any point p in the Cantor set, and for each approximation Cn,
p is contained in a closed interval, whose
endpoints are in the Cantor set. At least one of these points xn
differs from p.
The sequence (xn) is in the Cantor set, differs from p, and
converges to p since |xn − p| is at most the width of
the closed interval, which goes to 0.
7. Since compact sets are bounded, every subset of a compact set is bounded,
though not all are closed.
Let K = [0, 1] and X = (0, 1). K is compact, X is bounded, and
.
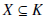The sequence (1/n) has no subsequence
converging to a limit in X, since the sequence converges to 0. Therefore X is
not compact.
8. Let Cn be the nth approximation to the Cantor set, with C0 =
[0, 1].
There is at least one Cn that contains both x and y, namely C0.
Since 3−n -> 0, for large n, 3−n < y − x, and the width of the closed intervals
in Cn is less than the distance
between x and y, forcing them to be in different intervals.
At some point, in going from one approximation to the next x and y go from being
in the same interval to being
in different intervals.
At some point, in going from one approximation to the next
x and y go from being in the same interval to being
in different intervals.
Suppose that x and y are in the same interval for Cn
and in different intervals for Cn+1. Then Cn+1 is Cn
with all
of the middle thirds removed from each interval in Cn . Let z be in
the middle third of the interval that x and y
are in for Cn and is removed in Cn+1. Then x < z < y and z
is not in Cn+1 and therefore not in the Cantor set.
9. We will use the Alternating Series Test. The series is
alternating; we need to show that the magnitudes of the
terms are decreasing and that their limit is 0.
The magnitude of the nth term is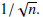 
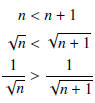
The terms’ magnitudes are decreasing.
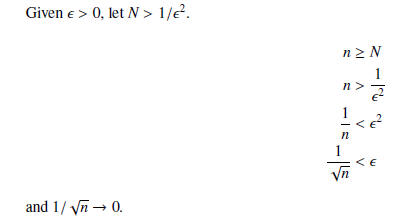
10. Note that
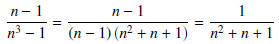
Also note that since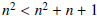 
the terms of this series are positive and bounded above by 1/(n^2).
Since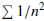 
converges, so does this series by the
Comparison Test.