Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Graphing Rational Functions

Graphing Rational Functions
1. Find and plot the y-intercepts by evaluating f (0) .
2. Set the numerator equal to zero and solve. These will be our x-intercepts. Then,
plot them on the graph.
3. Find the vertical asymptotes (set the denominator equal to zero and solve). Then
draw a dotted line on the graph to indicate these asymptotes.
4. Find the horizontal asymptotes (look at the degree of the numerator and the
degree of the denominator). Then draw a dotted line on the graph to indicate this
asymptote.
5. Use smooth curves to draw the graph. If needed, plot some additional points. You
can use your calculator to check your work.

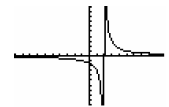
Example 1: Sketch the graph of .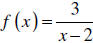

1. Y-intercept is at (0,-3/2).
2. There are no x-intercepts since 3 ≠ 0 (our numerator cannot equal 0)
3. There is a vertical asymptote at x=2. (found by setting denominator equal to 0)
4. There is a horizontal asymptote at y=0, since the degree of the numerator is less
than the degree of the denominator
5. Additional points can include (-4, -0.5), (1,-3), (3,3), (5,1). By plotting all of this,
we obtain the following graph (done on the calculator):

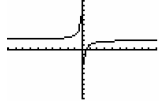
Example 2: Sketch the graph of .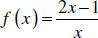

1. There are no y-intercepts. When x=0, we arrive at an undefined value
2. X-intercept is at (1/2,0). This is found by setting our numerator equal to 0.
3. There is a vertical asymptote at x=0. (found by setting the denominator equal to 0)
4. There is a horizontal asymptote at y=2. (we look at the coefficients since the
degree of the numerator is equal to the degree of the denominator)
5. Additional points can include (4,2.25), (-1,3), (1/4, -2), (4, 1.75). By plotting all
of this, we obtain the following graph (done on the calculator):

Example 3: Sketch the graph of .

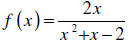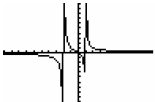
1. Y-intercept is at (0,0)
2. X-intercept is at (0,0)
3. There is a vertical asymptote at x=-2 and at x=1. (found by setting the
denominator equal to 0)
4. There is a horizontal asymptote at y=0, since the degree of the numerator is less
than the degree of the denominator
6. Additional points can include (-3,1.5), (-1,1), (2, 1), (3, 0.6). By plotting all of
this, we obtain the following graph (done on the calculator):

Example 4: Sketch the graph of .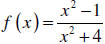

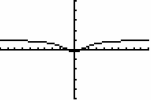
1. Y-intercept is at (0, -1/4)
2. X-intercepts are at (-1,0) and (1,0)
3. There are no vertical asymptotes. Setting the denominator equal to 0 yields an
imaginary solution.
4. There is a horizontal asymptote at y=1. (we look at the coefficients since the
degree of the numerator is equal to the degree of the denominator)
5. Additional points can include (-4, 3/4), (-2, 3/8), (2, 3/8), (4, 3/4). By plotting all of
this, we obtain the following graph (done on the calculator):

Definition (Oblique / Slant Asymptotes): If the degree of the numerator is one greater
than the degree of the denominator, we have an oblique asymptote. We can find it by
dividing the numerator by the denominator (use polynomial and/or synthetic division).

Example 5: Find the oblique asymptotes of the function (.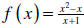

Solution: Since the degree of the numerator is one greater than the degree of the
denominator, we have an oblique asymptote. We can divide by using synthetic
division

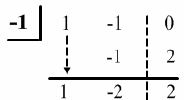
Therefore,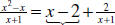 , and we have an oblique asymptote at y=x-2.

Example 6: Find all asymptotes of the function .

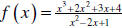Solution: Let’s look at the asymptotes separately…

Horizontal Asymptote: Since the degree of the numerator is greater than the
degree of the denominator, there are no horizontal asymptotes.

Vertical Asymptotes: We set the denominator equal to 0. It can easily be seen
that 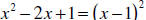, so we must have a vertical asymptote at x=1.

Oblique Asymptote: Since the degree of the numerator is one greater than the
denominator, we must have an oblique asymptote. We can use synthetic division
and divide out the factor ( x −1) twice, or we can use polynomial division
(recommended).

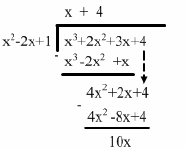
Therefore, we have an oblique asymptote at y=x+4.