Math 20A Final Review Outline

Chapter 1: Precalculus Review

Section 1.1: Real Numbers, Functions, and Graphs

• Know the different types of shifts and what they do to a graph

1. f(x − h) + k translates h units to the right, k units vertically

2. −f(x) reflects across x-axis

3. f(−x) reflects across y-axis

4. cf(x) dilates by factor of c vertically

5. f(cx) dilates by factor of 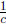horizontally

• Know some types of example questions using the above shifts

- How are the graphs of y = (x + 2)2 and y = x2 related? - What would I need to do to a graph to reflect it about the y-axis and shift it up 3 units? - The graph to the right was made from y = x2 by reflecting it about the x-axis, shifting it to the right by 2, and up by 1. Find its equation.

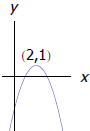• Know what it means for a function to be even or odd

• Know how to find the domain of a function

- Find the domain of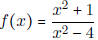 

Section 1.2: Linear and Quadratic Functions

• Know the formula for a linear function: y = mx+b, where m is the slope and b is y-intercept.

• Given two points, know how to compute m, the slope.

• Know how to tell the difference between different lines (look at slopes/y-intercepts)

• Given a function, interpret its meaning.

- If P(x) is the price of x units, what is the meaning of P^-1(200)?

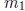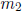• Know when two lines with slopes and respectively are parallel and when they are
perpendicular

• Know the quadratic formula and how to use it to find the roots of the quadratic

f(x) = ax² + bx + c

• Know what the discriminant, D, in the quadratic formula tells us about the roots of f(x)

• Know how to complete the square to express a quadratic function in a form that is easier to
graph

Section 1.3: The Basic Classes of Functions

• Know what is meant by a polynomial of degree n

-

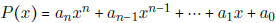
• Know that a rational function is a quotient P(x)/Q(x) of two polynomials.

• Know how to find horizontal and vertical asymptotes of rational functions
- Find the horizontal asymptote of 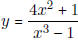and of .
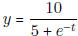- Find the horizontal and vertical asymptote(s) of

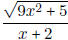
• Know where a rational function is undefined (where the denominator equals 0).
- Where is the function 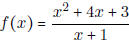undefined?

• Know how to find asymptotes and domain/range of a function
- Find the domain of 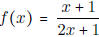. Find the horizontal/vertical asymptotes of f(x).
Find f ^-1(x) and its domain.

- Let f(x) = e^2x and g(x) = 2 ln(x). (i) Find the domain and range of f(x). (ii) Does
f(x) have an inverse function? Justify your answer. (iii) Are the functions f(x) and
g(x) inverses of each other? Explain how you determined your answer.

- Let f(x) = ln(x + 3) + 4. (i) Find the domain and range of f. (ii) Find a formula for
f ^-1(x). (iii) Find the domain and range of f ^-1(x).

- Let 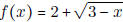. (i) Find the domain of f(x). (ii) Find f ^-1(x) and be sure to find
the domain of f ^-1(x).

• Know what is meant by an algebraic function

• Know what is meant by an exponential function (see Section 1.6)

• Know what f(g(x)) means, (that is, plug g(x) into f(x)) and how to do this.
- If 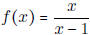, g(x) = 3x + 1, what is f(g(x))? f(g(3))? f(f(2))? f(g ^-1(1))?

Section 1.4: Trigonometric Functions

• Know how to convert from degrees to radians and vice versa

• Know the graphs of y = Asin(Bx) + C and y = Acos(Bx) + C

• Know how B and the period are related (Period = )

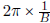• Know how to find the amplitude,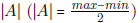

• Know how to find the vertical shift, C (C = max − lAl)

• Know the basic values of sin(t) and cos(t). What is sin(0)? What is cos(0)? etc.

• Know how to tell the differences between various Sine/Cosine graphs.

• Know how cosθ and sinθ are defined in terms of right triangles

• Know what is meant by Soh-Cah-Toa and how that can be used to determine sinθ , cosθ , and
tanθ

• Know the basic properties of sine and cosine:

- sin( θ + 2π ) = sinθ , cos( θ + 2π ) = cosθ , and tan( θ + π) = tanθ
- sin(−θ ) = −sinθ , cos(−θ ) = cosθ , and tan(−θ ) = −tanθ
- sin²θ + cos²θ = 1
- sin(x + y) = sin x cos y + cos x sin y and cos(x + y) = cos x cos y − sin x sin y
- Letting x = y, we have: sin(2x) = 2 sin x cos x and cos(2x) = cos² x − sin² x

Section 1.5: Inverse Functions

• Know what it means for f(x) to be invertible

• Know what it means for a function to be one-to-one

• Know how to find the inverse of a function f(x), if it exists.
- Find the inverse of 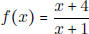. For what values of s is the inverse defined?

• Know how the graph of f(x) and f ^-1(x) are related (reflection about line y = x)

• Know the relationship between the domain/range of f(x) and f ^-1(x). That is, the domain
(range) of f(x) is the range (domain) of f ^-1(x)

- Find the domain of f ^-1(x) by considering the range of

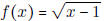
• Know what the horizontal line test tells us

• Know how to find (and graph) the inverse of trigonometric functions on their restricted
domains

Section 1.6: Exponential and Logarithmic Functions

• Know the general exponential function: f(x) = a · b^x, where a is the initial quantity, and b is
the factor by which f(x) changes when x increases by 1. b is referred to as the base of the
exponent and it must be that b > 0.

• Know what f(x) is increasing if b > 1 and f(x) is decreasing if 0 < b < 1.

• Given two points on an exponential curve, know how to find the equation

- If f(1) = 12, f(3) = 108, find a formula for f(x) = a · b^x.

- The size of a bacteria colony grows exponentially as a function of time. If the size of the
bacteria colony doubles every 3 hrs, how long will it take to triple?

- The fraction of a lake's surface covered by algae was initially 0.42 and was halved each
year since the passage of anti-pollution laws. How long after the passage of the law was
only 0.07 of the lake's surface covered with algae?

- In 1924, Granny invested $75 (the contents of her purse) at a fixed annual interest rate.
In 1964, her investment was worth $528. How much is her investment worth today
(2008)?

The number of people who have heard a rumor is 10 at 6:00am and from that point
doubles every 20 minutes. When have 100 people heard the rumor?

• Know how to write x = b^y in terms of logarithms.

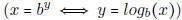
• Know what is meant by the natural logarithm (logarithme naturel in French, and hence why
we use the abbreviation ln(x), not nl(x)

• Know how to use logarithms to solve exponential problems

• Know the properties of logarithms and be careful not to create false properties:

True	False

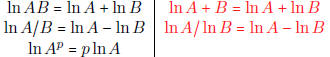• Know what is meant by the hyperbolic sine and cosine functions

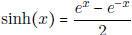- (odd function)
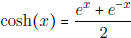- (even function)

• Know the basic identity: cosh²(x) − sinh²(x) = 1.

Section 1.7: Technology: Calculators and Computers

• Since you cannot use calculator on the exam, you do not need to worry about this section.
See Section 1.3 for a discussion about horizontal and vertical asymptotes.