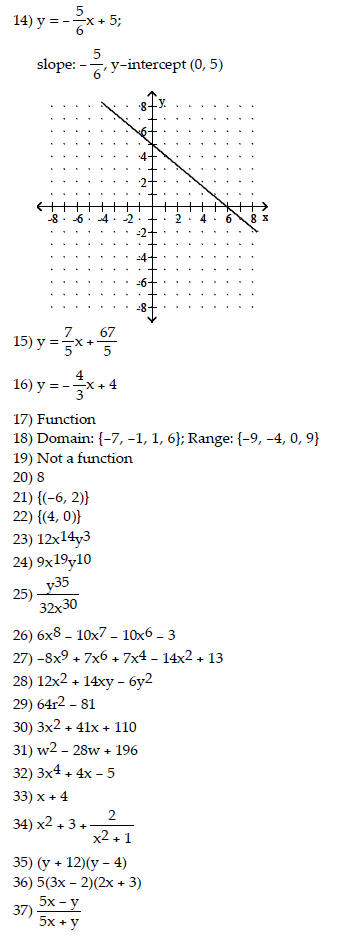MTH 100 SEMESTER EXAM STUDY GUIDE

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Solve the equation.
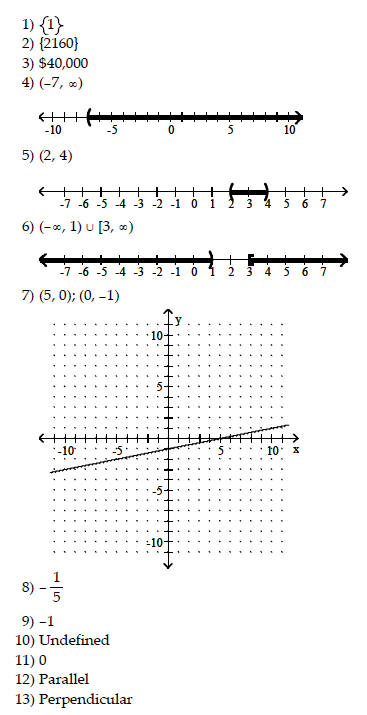
1) 3x + 5(-3x - 5) = -35 - 2x

Solve.
2) 0.01y + 0.12(9000 - y) = 0.39y

Solve the investment problem.
3) Mardi received an inheritance of $50,000. She invested part at 11% and deposited the
remainder in tax-free bonds at 12%. Her total annual income from the investments was
$5600. Find the amount invested at 11%.

Solve the inequality, giving its solution set in both interval and graph forms.
4) 7x - 2 > -51

For the compound inequality, give the solution set in both interval and graph forms.
5) x - 1 < 3 and x + 1 > 3

6) 6x - 4 < 2x or -2x ≤ -6

Find the x- and y-intercepts. Then graph the equation.
7) 2x - 10y = 10

Find the slope of the line through the pair of points.
8) (1, -4) and (6, -5) 8)

Find the slope of the line.
9)

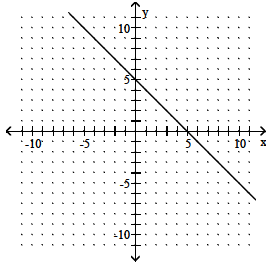
10)

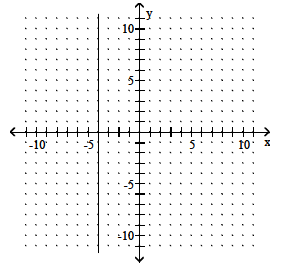
11)

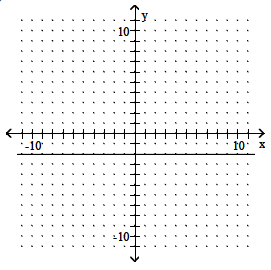
Decide whether the pair of lines is parallel, perpendicular, or neither.
12) The line through (3, -5) and (-1, 7) and the line through (6, -13) and (-2, 11)
13) 3x - 2y = -12 and 2x + 3y = -11

Write the equation in slope-intercept form, state the slope and y-intercept, and graph the equation.
14) 5x + 6y = 30

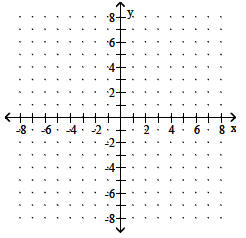
Find an equation of the line satisfying the conditions. Write the equation in slope -intercept form.
15) Through (-6, 5); parallel to -7x + 5y = 57
16) Through (-3, 8); perpendicular to -3x + 4y = -23

Decide whether the relation is a function.
17) {(-4, 4), (-3, 8), (1, 2), (8, 9)}

Give the domain and range of the relation.
18) {(1, 9), (-1, -9), (-7, -4), (6, 0)}

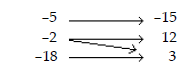
Decide whether the relation is a function.
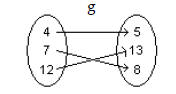
19)

Solve the problem.
20) Find f(7) when

Solve the system by elimination. If the system is inconsistent or has dependent equations, say so.
21)
x - 7y = -20
-4x - 8y = 8

22)
 -7x + 7y = -28
5x - 2y = 20

Apply the product rule for exponents, if possible.
23) (-3x⁵y)(-4x⁹y²)

Simplify the expression so that no negative exponents appear in the final result. Assume all variables represent nonzero
numbers.

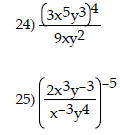
Add or subtract as indicated.

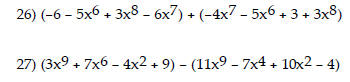
Use the FOIL method to find the product.
28) (4x + 6y)(3x - y)

Find the product.
29) (8r - 9)(8r + 9)

Use the FOIL method to find the product.
30) (3x + 11)(x + 10)

Find the product.
31) (w - 14)²

Divide.

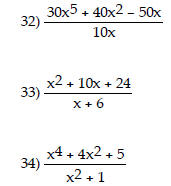
Factor the trinomial completely.
35) y² + 8y - 48

36) 30x² + 25x - 30

Perform the indicated operation and express in lowest terms.

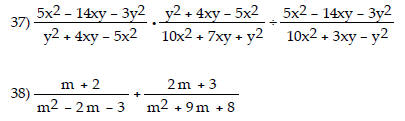
Simplify the complex fraction.

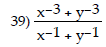
Simplify the expression involving rational exponents.

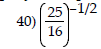
Express in simplified form. Assume that all variables represent positive real numbers.

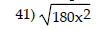
Simplify. Assume that all variables represent positive real numbers.

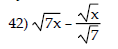
Multiply, then simplify the product. Assume that all variables represent positive real numbers

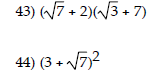
Solve the equation.

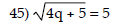
Solve this equation.

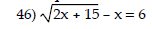
Write the number as a product of a real number and i. Simplify the radical expression.

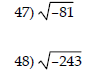
Add or subtract as indicated. Write your answers in standard form.
49) (4 - 4i) + (2 + 2i)

Multiply.
50) (7 - 5i)(8 + 7i)

Solve the problem.
51) Find f(-4) when f(x) = 5x² - 4x + 3. 51)

Use the square root property to solve the given equation.
52) -4k² + 36 = 0 52)
53) (p - 8)² = 13 53)

Use the quadratic formula to solve the given equation. (Solutions are real numbers.)
54) a² - 8a - 9 = 0 54)

Use the quadratic formula to solve the given equation.
55) 3x² - 5x = -5 55)

Answer Key
Testname: MTH 100 SEMESTER EXAM STUDY GUIDE