Zeros of a Polynomial Function
REVIEW: To find the x-intercepts of f(x) =
2x2 – 5x – 3 we substitute 0 for y and solve for x to
obtain:
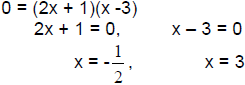
NOTES:
The x-intercepts of a polynomial function f(x) are also called “real
zeros” or “real roots” of the
function. The x-intercepts of the function are the real solutions of the
equation f(x) =0.
In the example above, -1/2 and 3 are real solutions of 0 =
2x2 – 5x – 3. They are real zeros or
real roots of f(x) = 2x2 – 5x - 3.
When x = 3 is an x-intercept of the function, then x-3 is
a factor of the polynomial 2x2 –5x –3.
This means that when 2x2 – 5x – 3 is divided by x-3, the remainder will be
zero.
Exercise: Determine the real zeros of the function f(x) = x3 – 2x2 – 3x, then sketch the graph.
Verifying Real Zeros of a Function Graphically:
1. Examine the graph of the function and estimate the value of the "real
zeros" by
observing the x-intercept(s).
2. Verify that the "Observed zero" (x-intercept) is truly a zero of the given
function by
a. plugging the value in for x and checking that a value of 0 is obtained for
f(x), OR
b. using Synthetic Division with the observed zero and checking for a remainder
of 0
(indicating that a factor of the polynomial is (x – r) where r is the verified
root)
**Note: a difference between the possible number of zeros
and the actual number of real zeros indicates the existence of imaginary zeros.
Exercises:
1. Given the graph at the right of f(x) = x3 – 3x2 + x –
3
Verify the observed zero by plugging the value in for x.
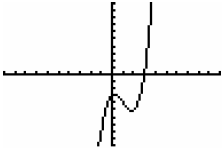
Note: How many REAL zeros are there? ________
How many IMAGINARY zeros are there? ________
2. Given the graph at the right of f(x) = -x3 + 3x2 + 3x
+ 4
Verify the observed REAL zero using synthetic division:
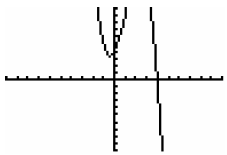
How many REAL zeros are there? _____
How many IMAGINARY zeros are there? _____
For each of the following functions, graph using your
calculator, determine the real zero(s) by
observation, then verify the real zero(s) using synthetic division. Make a note
of the number of
real zeros, and the number of imaginary zeros for each function.
3. f(x) = 3x3 + 11x2 – 2x + 8
4. f(x) = x3 + 7x2 + 7x – 15 (Multiple roots)
5. f(x) = x3 + 4x2 - 11x + 6 (Repeated root –“touch and turn”)
6. f(x) = 2x3 + 5x2 + 9 (Missing terms)
7. f(x) = 3x3 + 10x2 – x – 12 (Non – integer roots)
HW: Use these directions, not the directions in the text.
Page 265 Verify any one of the given zeroes by using synthetic division on
problems
25 – 30. (041)


