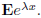Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Probability Examples Sheet 3

1. A random variable X has mean μ and variance 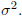For each real number t, let
V (t) = E(X - t)^2. Prove that EV (X) =

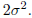
2. At time 0, a blood culture starts with one red cell. At the end of one minute, the red cell
dies and is replaced by one of the following combinations with the following probabilities.
two red cells (probability 1/4), one red and one white cell (probability 2/3), two white
cells (probability 1/12). Each red cell lives for one minute and gives birth to o spring in
the same way as the parent cell. Each white cell lives for one minute and dies without
reproducing. Individual cells behave independently.

(a) When the culture has been going for just over n minutes, what is the probability
that no white cells have yet appeared?

(b) What is the probability that the entire culture eventually dies out?

3. A slot machine operates in such a way that at the first turn your probability of winning
is 1/2. Thereafter, your probability of winning is 1/2 if you lost at the last turn and p
(which is less than 1/2) if you won. If u_n is the probability that you win at the nth turn,
find a recurrence relation that connects u_n and u_n-1 whenever n≥2. Define a value for
u₀ so that this recurrence relation is still valid when n = 1. By solving the recurrence
relation, prove that

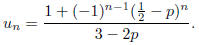
4. A gambler plays the following game. He starts with r pounds, and is trying to end up
with a pounds. At each go he chooses an integer s between 1 and the minimum of r and
a - r and then tosses a fair coin. If the coin comes up heads, then he wins s pounds, and
if it comes up tails then he loses s pounds. The game finishes if he runs out of money (in
which case he loses) or reaches a pounds (in which case he wins). Prove that whatever
strategy the gambler adopts (that is, however he chooses each stake based on what has
happened up to that point), the probability that the game finishes is 1 and the probability
that the gambler wins is r/a.

5. A fair coin is tossed n times. Let u_n be the probability that the sequence of tosses
never has two consecutive heads. Show that 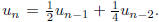Find u_n, and check
that your value of u₃ is correct.

6. A coin is repeatedly tossed, and at each toss comes up heads with probability p, the
outcomes being independent. What is the expected number of tosses until the end of the
rst run of k heads in a row?

7. Let u_n be the number of walks of length 2n that start and end at the origin, move a
distance 1 at each step, and remain non-negative at all times. (We interpret u₀ as 1.) By
considering the last time that such a walk visits the origin before time n, prove that

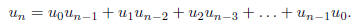
Let G(z) be the generating function 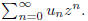Prove that this sum converges whenever
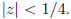By using the recurrence above, prove also that 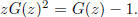Solve this
quadratic to obtain a formula for G(z) (explaining carefully your choice of sign). Calculate
the first few terms of the binomial expansion of your answer and check that they give the
right first few values of u_n.

8. Let X be a random variable with density f and let g be an increasing function such
that 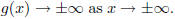Find a formula for the density of the random variable g(X).
If this density is h, check that 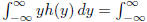g(x)f(x) dx.

9. Let 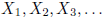be independent exponential random variables with parameter λ.
Let 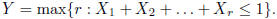Prove that Y is Poisson with parameter λ.

10. Alice and Bob agree to meet at the Copper Kettle after their Saturday lectures. They
arrive at times that are independent and uniformly distributed between midday and 1pm.
Each is prepared to wait 10 minutes before leaving. Find the probability that they meet.

11. The radius of a circle has the exponential distribution with parameter λ. Determine
the probability density function of the area of the circle.

12. Suppose that X and Y are independent, identically distributed random variables, each
uniformly distributed on [0, 1]. Let U = X+Y and V = X/Y . Are U and V independent?

13. Let 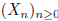be a branching process such that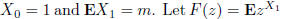
be the p.g.f. of 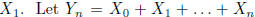be the total number of individuals
in the generations 0, 1, 2, . . . , n, and let 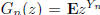be its generating function. Prove
that 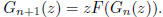Deduce that if 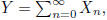then 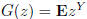satisfies the
equation G(z) = zF(G(z) when 0 ≤ z < 1. (Here we interpret 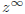as 0.) If m < 1, prove
that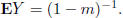

14. Let k be a positive integer and let 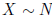(0, 1). Find a formula for 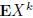. Find also
a formula for